multiple followers
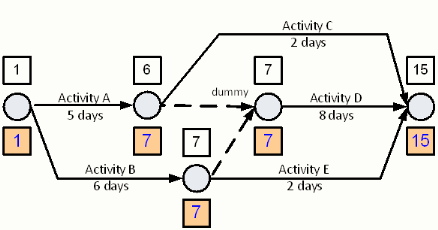
Now consider the schedule shown below. Notice the two logic dummies shown as activities 10-20 and 15-20. The forward pass is already completed for this schedule resulting in an early event time at node 25 of day 15.
The backward pass begins by setting the last nodeís Late Event Time to the nodesí Early Event Time. In the example schedule above, node 25ís Late Event Time is set to day 15. We can now begin the backward pass calculation. Begin with Activity D. The Late Event Time at node 20 is the Late Event Time at node 25 less the duration of Activity D, 8 days. Therefore, the Late Event Time at node 20 is 7.
In selecting the next activity and node through which the Backward Pass is to be calculated, there is a problem. Node 10 and node 15 both have more than one possible Late Event Time. Node 10ís Late Event Time could either be 13 or 7. The value of 13 is obtained by subtracting the duration of Activity C from the Late Event Time of Activity C. The value of 7 is obtained by subtracting the duration of the dummy activity (nodes 10-20), which is by definition set to zero, from the Late Event Time of node 20.
Thinking about the objective of the Backward Pass can assist in deciding which of the two incoming Late Event Times for node 10 to select. The objective of the Backward Pass is to find the latest time possible that an event can occur and not delay the schedule. Letís now consider node 10. If we complete node 10 on day 13 what will be the impact on the start of Activity D? The impact is that the end of Activity D would not occur until 13 plus 8 days, i.e. day 21. This is a 6 day delay past when the Activity D could end.
So what does the discussion above tell us about which of the incoming Late Event Time values should be selected during the backward pass? It tells us that the value we should select is the earliest of any incoming Late Event Times.
Letís check this rule. If node 10 is set to 7, the earliest of the incoming values, then Activity D completes on day 15, without delaying the completion of Activity D.
Notice that if Activity C begins on day 7 that it will be completed on day 9. We will discuss the difference between Activity Cís possible completion time and the time calculated here in the section on Float.
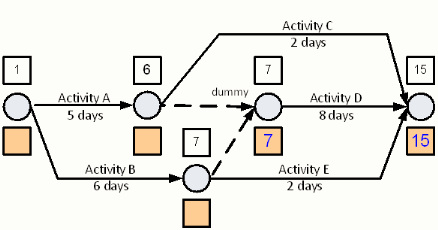
For now, letís complete the calculation of the backward pass through each of the remaining activities. The figure below shows the full result.